人数分布や度数パターンにおける相違を検討する際に用いる。
定性的データにおいて、その標本において生じている差異が、母集団においても認められるか(有意な差であるか)推測するための分析である。
例えば20人を対象にある質問を行い、賛成が15人、反対が5人いたとする。
このとき、15人と5人の差10は大きく見えるが、この差が調査対象の20名(標本)だけでなく、調査対象となりえる全ての人(母集団)に対しても差があるといえるか、20名のデータから推測する。実際にχ²検定を行うとχ²=5.00、p=.025という数値が得られ、「有意な差がある」とされる。
このような分析は2変量でも行われ、例えば、賛成-反対に加え、回答者の性別データが得られている場合の意見の相違についても分析が可能である。
| 男性 | 女性 | 意見合計 | |
| 賛成 | 5 | 14 | 19 |
| 反対 | 15 | 6 | 21 |
| 性別合計 | 20 | 20 | 40 |
定量的データ間に、直線的な関係がどの程度あるか検討するための分析である。
例えばテストを行い、算数の得点を縦軸、国語の得点を横軸にとったとする。
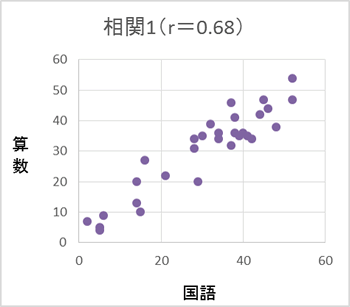
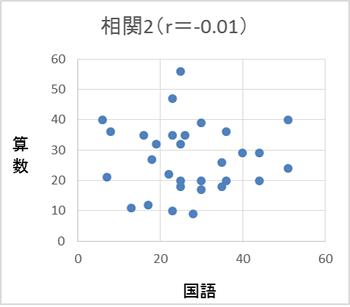
紫色でプロットされたグラフ(相関1)は算数の得点が高いとき国語の得点も高く、青色でプロットされたグラフ(相関2)は算数の得点が高くても国語の得点は高かったり低かったりしている。紫のグラフ(相関1)のような直線的な関係がどの程度みられるのかの指標である「相関係数」を算出するのが相関分析である(グラフタイトルでrで示している)。
多くの分析では、データが正規分布に従うことを前提としているため、正規分布していないデータを分析する際には望ましくない検定も存在する。そのため、t検定などの前にはそれぞれのグループが正規分布に従うかどうか、Kolmogorov-Smirnov検定で検討する。
2群間で得られた定量的データに差があるか検討する際に用いる。
2群が正規分布に従うか、2群間に対応があるかによって分析方法に違いがあり、必ずしもt検定を使用しないが、大まかに「差の検定」としてひとくくりにされることも多い。
例えば健康診断において、週2回以上運動をしているグループ15名とそうでないグループ15名で体脂肪率を比較するとする。このデータでt検定を行うと、t(28)=-1.41、p>.05の結果が得られ、運動の有無による体脂肪率には有意な差はないといえる。
| 運動あり | 運動なし | |
| 1人目 | 26 | 27 |
| 2人目 | 19 | 20 |
| 3人目 | 27 | 16 |
| 4人目 | 20 | 25 |
| 5人目 | 20 | 20 |
| 6人目 | 27 | 28 |
| 7人目 | 29 | 34 |
| 8人目 | 18 | 17 |
| 9人目 | 28 | 28 |
| 10人目 | 29 | 38 |
| 11人目 | 15 | 21 |
| 12人目 | 20 | 23 |
| 13人目 | 18 | 33 |
| 14人目 | 21 | 19 |
| 15人目 | 18 | 31 |
カテゴリーが3つ以上に分けられるグループ間で定量的データに差があるか検討する際に用いる。データの正規分布の有無や対応の有無により異なる分析を行うが、大まかにひとくくりにされることがある。
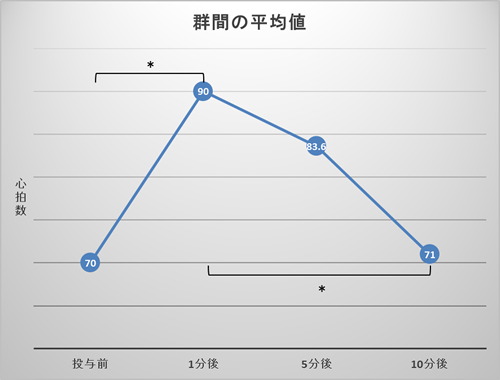
例えば、ある薬物を投与することで心拍数に変化がみられるかどうかを、数回にわたって心拍数を計測することで調べたとする。これは今までのデータと異なり、同一人物に対して繰り返しデータを収集しているため、対応のあるデータとして分析を行う。
| 投与前 | 1分後 | 5分後 | 10分後 | |
| Aさん | 67 | 92 | 87 | 68 |
| Bさん | 92 | 112 | 94 | 90 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
| Lさん | 61 | 90 | 83 | 66 |
| Mさん | 72 | 85 | 72 | 69 |
このデータを分析するとF(3,12)=17.50、p<.001の結果が得られ、有意な差があるといえるが、この結果は「投与前、1分後、5分後、10分後のどこかに有意な差がある」ことだけが明らかな状態である。具体的にどこに差があるのか検討するための多重比較を行い全ての組み合わせについて分析すると、結果として投与前と投与1分後、および投与1分後と10分後の間にそれぞれp<.05の有意な差があることが明らかになる。
2つの定性的データ間の定量的データに差があるか検討するための分析である。対応の有無により異なる分析を行うが、大まかにひとくくりにされることが多い。
例えば、ある講習に参加した人物60名について、講習後に意識調査を行ったとする。
|
ID |
得点 |
内容 |
職種 |
|
1 |
10 |
A |
人事 |
|
2 |
15 |
B |
企画 |
|
3 |
20 |
B |
企画 |
|
4 |
24 |
B |
総務 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
|
58 |
20 |
B |
企画 |
|
59 |
32 |
A |
人事 |
|
60 |
16 |
A |
経理 |
この意識調査で得られたのは、意識に関する得点データと、講習内容と、回答した人物の職種であった。
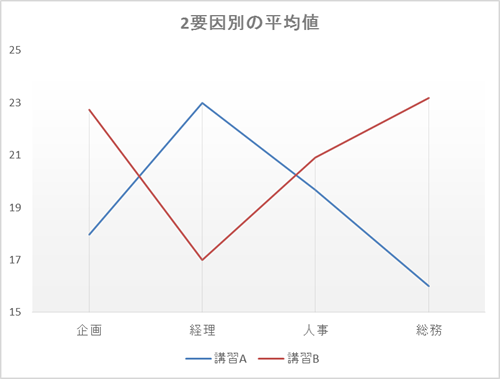
2要因の分散分析では、講習内容と職種の2種類の定性的データを組み合わせた場合の複合効果としてあらわれる差異(交互作用)と、それぞれの定性的データをそれぞれ独自にみた時の定量的データの差異(主効果)を検討する。
結果、交互作用がみられる場合は平均値をとると下のようなグラフが得られ、講習を1つに限定したときの職種による得点の差異と、職種を1つに限定したときの講習による得点による差異(単純主効果)の検定を行うことになり、それぞれの条件においてどのペアで差異がみられるか検討がなされる。その結果をまとめたのが以下の表である。
|
講習 |
不等号 |
有意確率 |
|||
|
A
|
企画 > 経理 |
.005 |
** |
||
|
企画 < 人事 |
.045 |
* |
|||
|
企画 総務 |
.055 |
||||
|
経理 > 人事 |
.013 |
* |
|||
|
経理 > 総務 |
.002 |
** |
|||
|
人事 > 総務 |
.013 |
* |
|||
|
B
|
企画 > 経理 |
.003 |
** |
||
|
企画 人事 |
.056 |
||||
|
企画 総務 |
.131 |
||||
|
経理 < 人事 |
.023 |
* |
|||
|
経理 < 総務 |
.003 |
** |
|||
|
人事 総務 |
.064 |
|
|||
|
p<.05*、p<.01** |
|||||
|
職種 |
不等号 |
有意確率 |
|||
|
企画 |
A < B |
.009 |
** |
||
|
経理 |
A > B |
.006 |
** |
||
|
人事 |
A B |
.563 |
|||
|
総務 |
A < B |
.013 |
* |
||
|
p<.05*、p<.01** |
|||||
複数の変数間の関係を探り、背景にある因子を見つけることが目的である。複数の観測されたデータがどのような潜在的な因子から影響を受けているか、情報を集約する際用いる。調査やアンケートの質問項目の処理に用いられることが多い。
例えば、社員の精神的な健康度を調査するため、質問項目を20項目作成し、「とてもあてはまる」「ややあてはまる」「あまりあてはまらない」「全然あてはまらない」の4段階で回答した80人分のデータがあるとする。
|
1 |
心配事があってよく眠れない。 |
|
2 |
仕事をする時、集中が続かない。 |
|
3 |
趣味を楽しむ時間が十分確保できている。 |
|
4 |
自分の人生は退屈だと思う。 |
|
・ ・ ・ |
・ ・ ・ |
|
17 |
イライラしてものごとが手につかない時がある。 |
|
18 |
仕事が思うように進まなくても、適切に対処できると思う。 |
|
19 |
ふと憂鬱になることがある。 |
|
20 |
ある程度期待通りの生活水準を手に入れていると思う。 |
これらの質問項目から、精神的な健康度のどのような側面が測定されているか明らかにするため、80名のデータを用いて因子分析を行った結果は以下の表のとおりである。因子分析では、因子の抽出方法が複数あることに加え、因子の数や分析から除外する項目について複数の解釈が可能なため、分析を何度も繰り返す必要があることが多い。
このデータを因子分析した初期解は①のとおりである。赤字で示した因子負荷量.35未満の項目と多重負荷のみられる項目を分析から除外し、再度分析しなおしたのが②である。
|
主因子法による因子分析、Promax回転① |
|||||
|
|
因子1 |
因子2 |
因子3 |
共通性 |
|
|
1.不安感(α=.86) |
|||||
| 項目12 |
.85 |
-.22 |
.00 |
.89 |
|
| 項目1 |
.76 |
-.03 |
.03 |
.87 |
|
| 項目16 |
.73 |
.05 |
.12 |
.76 |
|
| 項目14 |
.64 |
-.13 |
.03 |
.55 |
|
| 項目13 |
.53 |
.16 |
.04 |
.49 |
|
| 項目5 |
.46 |
-.23 |
.17 |
.43 |
|
| 項目11 |
.39 |
-.46 |
.19 |
.33 |
|
| 項目17 |
.31 |
-.21 |
.13 |
.22 |
|
|
2.満足感(α=.81) |
|||||
| 項目9 |
-.13 |
.72 |
-.24 |
.76 |
|
| 項目3 |
-.03 |
.68 |
-.13 |
.64 |
|
| 項目20 |
-.05 |
.63 |
-.12 |
.48 |
|
| 項目4 |
.09 |
.-54 |
-.21 |
.46 |
|
| 項目8 |
-.42 |
.43 |
-.13 |
.39 |
|
| 項目2 |
.13 |
-.30 |
-.04 |
.26 |
|
| 項目19 |
.16 |
-.29 |
-.02 |
.16 |
|
|
3.不全感(α=.76) |
|||||
| 項目10 |
-.13 |
.13 |
.68 |
.55 |
|
| 項目7 |
.01 |
-.03 |
.64 |
.52 |
|
| 項目18 |
-.06 |
.23 |
-.56 |
.49 |
|
| 項目15 |
.03 |
-.26 |
.43 |
.34 |
|
|
項目6 |
-.06 |
.19 |
.33 |
.30 |
|
|
因子間相関 |
-.25 |
.06 |
|||
|
-.35 |
|||||
|
主因子法による因子分析、Promax回転② |
|||||
|
|
因子1 |
因子2 |
因子3 |
共通性 |
|
|
1.不安感(α=.87) |
|||||
| 項目12 |
.86 |
-.21 |
.00 |
.90 |
|
| 項目16 |
.79 |
-.03 |
.02 |
.87 |
|
| 項目1 |
.72 |
.03 |
.10 |
.73 |
|
| 項目14 |
.66 |
-.12 |
.03 |
.51 |
|
| 項目13 |
.55 |
-.18 |
.05 |
.43 |
|
| 項目5 |
.40 |
-.20 |
.12 |
.37 |
|
|
2.満足感(α=.80) |
|||||
| 項目9 |
-.12 |
.77 |
-.21 |
.74 |
|
| 項目3 |
.02 |
.70 |
-.11 |
.64 |
|
| 項目20 |
.04 |
.64 |
-.12 |
.51 |
|
| 項目4 |
-.11 |
-.53 |
-.19 |
.43 |
|
|
3.不全感(α=.77) |
|||||
| 項目10 |
-.11 |
.09 |
.68 |
.61 |
|
| 項目7 |
.03 |
.06 |
.67 |
.52 |
|
| 項目18 |
-.10 |
-.12 |
.-54 |
.48 |
|
|
項目15 |
.09 |
-.16 |
.46 |
.36 |
|
|
因子間相関 |
-.12 |
.07 |
|||
|
-.31 |
|||||
②の表から、項目1,5,12,13,14,16が不安感を測定する項目、項目3,4,9,20が満足感を測定する項目、項目7,10,15,18が不全感を測定する項目であることが明らかになった。
ある変数を用いてある変数を説明することが可能か検討し、データの予測を試みるのが回帰分析である。一つの変数から一つの変数を説明するのが単回帰分析、複数の変数から定量的データを説明するのが重回帰分析、複数の変数から定性的データを説明するのがロジスティック回帰分析である。回帰分析では、使用する変数の選択について複数の解釈が可能なため、分析を何度も繰り返すことがある。
例えば、ある大学で200名を対象に進路調査を行い、内定の有無をいくつかの変数で説明できるか検討した。得られたデータは性別、学部、一般教養科目の成績の最頻値、専門科目の成績の最頻値、エントリー社数、説明会参加回数、希望職種であった。このとき、説明されるデータである内定の有無は定性的データなので、使用するのはロジスティック回帰分析である。
|
ID |
性別 |
学部 |
一般科目 |
専門科目 |
エントリー社数 |
説明会参加数 |
希望職種 |
内定有無 |
|
1 |
女性 |
文学 |
B |
B |
50 |
18 |
事務 |
有 |
|
2 |
女性 |
教育学 |
B |
B |
34 |
10 |
一般 |
無 |
|
3 |
男性 |
工学 |
A |
B |
26 |
3 |
技術 |
有 |
|
4 |
男性 |
経済学 |
A |
A |
15 |
5 |
一般 |
無 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
|
197 |
男性 |
文学 |
S |
A |
9 |
7 |
事務 |
有 |
|
198 |
女性 |
教育学 |
C |
A |
13 |
2 |
事務 |
有 |
|
199 |
女性 |
経済学 |
B |
A |
37 |
16 |
一般 |
無 |
|
200 |
男性 |
経済学 |
B |
S |
26 |
12 |
技術 |
有 |
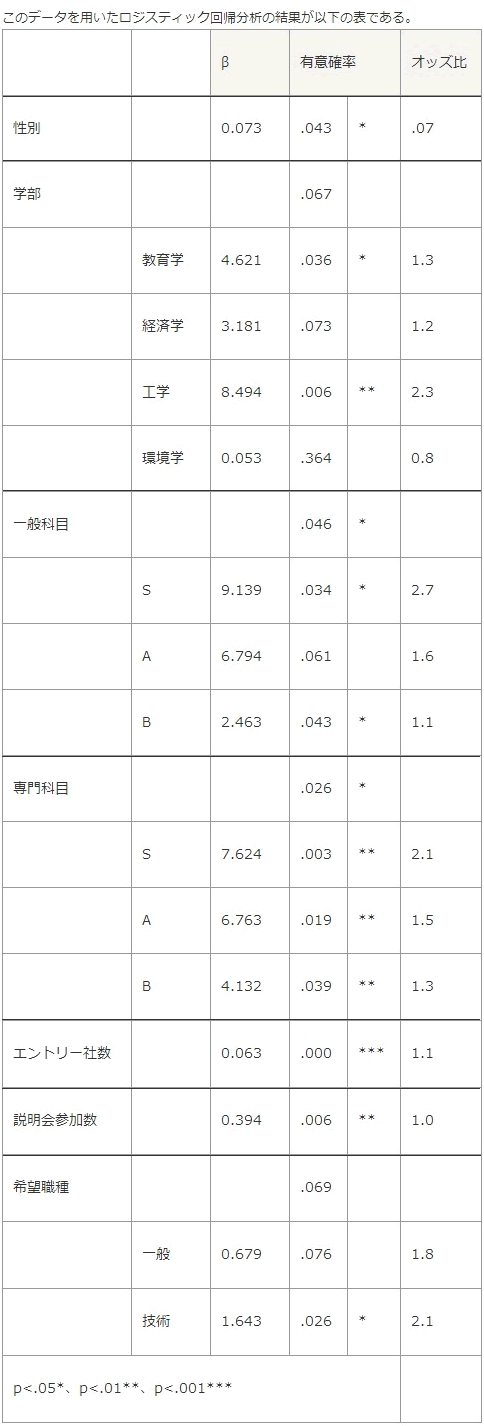
回帰分析では、それぞれの変数が与える影響の大きさの他、そのモデル全体でどの程度の説明力を持つかの指標(決定係数)なども加味して最終的なモデルを決定する。
| そば | うどん | 定食 | 丼もの | |
|
20代女性 |
8 |
5 |
3 |
3 |
|
30代女性 |
7 |
4 |
4 |
2 |
|
40代女性 |
7 |
6 |
1 |
2 |
|
50代女性 |
4 |
9 |
1 |
1 |
|
20代男性 |
3 |
3 |
9 |
7 |
|
30代男性 |
2 |
5 |
7 |
8 |
|
40代男性 |
3 |
4 |
6 |
7 |
|
50代男性 |
2 |
5 |
3 |
4 |
|
60代以上 |
6 |
8 |
2 |
1 |
対応分析とも呼ばれ、視覚的に定性データ間の関係を記述するために用いる。検定による母集団での差異の有無ではなく、図の描画が目的である。
例えば飲食店が行ったアンケートで、注文したメニューと利用者について上のような結果が得られたとする。このデータをもとにコレスポンデンス分析を行うと、以下のような図が得られる。
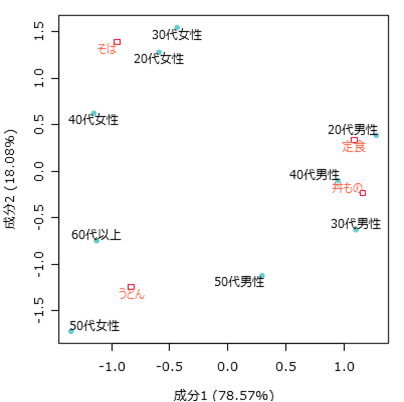
それぞれの変数間の距離が近いほど関連が強いことが示されており、原点からの距離が近いほど特徴が少ないことを表している。